常见信号频谱记忆小妙招

余弦信号

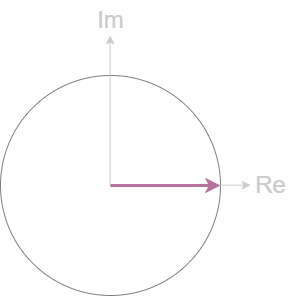
余弦信号是傅里叶变换的基（余弦信号和复指数信号$e^{j\Omega t}$性质相同，或者说复指数信号是余弦信号在复频域的推广），它的频谱非常纯粹，纯粹到只有正负频率上的两个冲激。

$$cos(\Omega_0 t)=Re[e^{j\Omega_0t}]=\frac{1}{2}(e^{j\Omega_0t}+e^{-j\Omega_0t})$$ $$cos(\Omega_0t)\leftrightarrow \frac{1}{2}[\delta(\Omega-\Omega_0)+\delta(\Omega+\Omega_0)]$$

将这两个冲激函数画在复平面上。

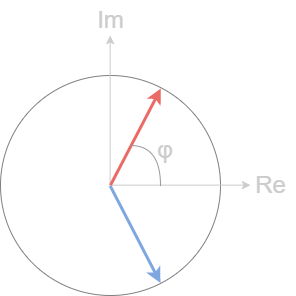
任意相位的余弦信号$cos(\Omega_0t+\phi)$频谱和$cos(\Omega_0t)$相似，频谱由两个纯粹的正负频率冲激构成，不过在复频域上添加了一点相移。

$$\begin{align} cos(\Omega_0 t+\phi ) &= Re[e^{j(\Omega_0t+\phi)}] \\ &= \frac{1}{2}(e^{j\phi }e^{j\Omega_0t}+e^{-j\phi }e^{-j\Omega_0t})\\ \therefore cos(\Omega_0t+\phi)&\leftrightarrow \frac{1}{2}[e^{j\phi }\delta(\Omega-\Omega_0)+e^{-j\phi}\delta(\Omega+\Omega_0)]\\ \end{align}$$

$$sin(\Omega_0t)\leftrightarrow \frac{1}{2j}[\delta(\Omega-\Omega_0)-\delta(\Omega+\Omega_0)]$$

$sin(\Omega_0t)$的频谱可以用$cos(\Omega_0t+\pi/2)$记忆。

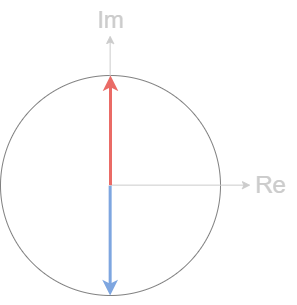
注意

1. 辅助圆的半径是冲激信号的大小1/2。
2. 该作图法只显示了冲激的大小和相位信息，没有频率。
3. 也可以用实信号频域共轭偶对称来记忆两个脉冲的关系。

门函数/矩形窗函数

三个参数确定一个门函数，长度$T$，幅度$A$，中心位置$T_0$

知道中心位置在原点的门函数频谱，其它门函数频谱乘一个时延因子$e^{-j\Omega T_0}$即可。

还是需要记忆频谱是$Sa$函数。

中心在原点的门函数是（共轭）偶对称函数，所以其频谱是实的。

$\Omega \rightarrow 0,Sa \rightarrow 1$，频率为0的分量是时域的直流分量——图形下的面积$AT$。确定频谱的形式是$ATSa$。

根据对偶性，频谱是频率为$-T/2\sim T/2$的余弦信号平权线性叠加，最高的频率是$T/2$，$Sa$内以$T/2$作为频率。更好的记忆方法还没有想到。

$$ATSa(\frac{T}2 \Omega )e^{-jT_0\Omega}$$