亚稳态和跨时钟域
⛏ 作者正在摸鱼,该推文尚未完成
何为稳态(Stable)?可以说,”稳”是对时间来说“平稳”,即相当长时间后,物体会趋于这一个状态保持不变。就如在碗中放入一个小球,小球来回滚动,最终会趋于碗底保持不动;也可以说,“稳”是对于干扰来说平稳,一种维持自身状态的能力,当小球位于碗底时,给予轻轻的扰动,小球会滚动几次慢慢恢复到碗底的位置。
flowchart LR a[暂态]-->|时间|b[稳态]
双稳态电路(Bistable)
最简单的双稳态电路由两个非门串联而成
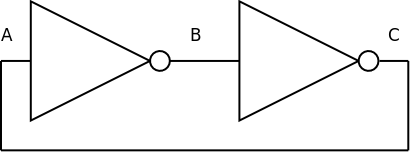
我们不妨称AB之间的非门为1号,另一个则是2号。
非门一般用CMOS工艺实现。
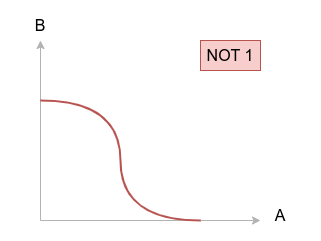
A也就是C(稳态下)
非门2的输入输出和非门1恰好相反。
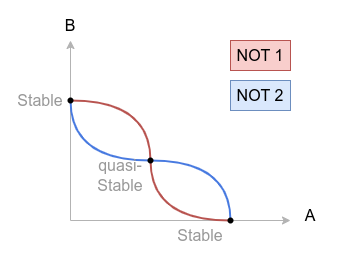
特性曲线仅有三个交点,也就是说,该电路有三个状态,随着时间流逝,电路状态一定会趋于这三个状态中的某一个。
其中和坐标轴相交的两个稳态对应着高低电平,将电平和比特相对应,我们知道双稳态电路可以储存1bit的信息量。中间的状态电平不高也不低,用来表示信息更容易失真,我们称之为亚稳态(quasi-stable)。
双非门的双稳态电路并不常用。比如初始电路状态A是低电平,此时我们让A变为高电平,暂态到稳态需要时间(或者说,信号的传输需要时间),这个瞬间B还是高电平,而CMOS非门由输入端控制两个互补MOS与电源和地之间通断实现,此时非门2导通的MOS一端接地,另一端接入C(A)高电平。导通的MOS管之间有一个不小的电压,会瞬时产生较大的电流。
这个例子也助于理解电路切换状态时瞬时功率较大
不过这个模型可以很好地引出亚稳态的概念。亚稳态来自于双稳态的对称性,可以推广到其他方法实现的双稳态电路之中。
电路利用反馈将状态趋近稳态点,若没有稳态对输出进行修正,多级电路将不断放大偏差,降低电路的准确性
那么电路最终趋于哪个稳态呢?在开头举了碗的例子,这是一个稳态。多个稳态也是类似的,想象弯弯曲曲的山谷,有谷峰,也有谷底。谷底就是稳态,多个稳态对应多个谷底。虽然具体过程不好分析,但从直观上,球的初始位置离哪个谷底近,大概率会落在那个谷底。
对于电路来说,若采样的电平很高或很低,能够很好地对应逻辑1和0,那么双稳态电路就能够趋近理想的稳态,而若采样的电平不高不低位置尴尬,就有可能掉入亚稳态的了。注意,三个状态都是平衡点,但只有稳态是稳定平衡,亚稳态是非稳定平衡。打个比方,亚稳态是山谷的“峰”,虽然峰顶平坦受力平衡,但只要轻轻一扰动,就会一发不可收拾滚下山峰。
也许这就是跨时钟域为什么要打两拍去除亚稳态的影响了
主从(Master-Slave)的采样
看来采样时机对电路状态至关重要,采样时机由什么决定呢?同步电路一般由触发器实现状态切换,而触发器离不开主从式结构。
每一个触发器,都是对前级信号采样,并对后级输出
TODO 传输门式结构
TODO 建立时间和保持时间
参考
感谢Y.D.X指出本文对于“稳态”“亚稳态”等概念叙述不太严谨,已对文章进行修改。——2023/3/6
