📢该推文部分内容是作者个人猜测,谨慎阅读。欢迎在评论区纠正!
⛏ 作者正在摸鱼,该推文尚未完成
微分方程往往是连续的,可计算机更偏好以离散的视角观察世界。如何用计算机求解微分方程?FDM给出了一种近似计算方法。
理论
✋Q:为什么要近似?知道解析式不能直接求出导数吗?
🧐A(个人猜测):MATLAB的符号函数可以实现求部分导函数解析式的功能了(并不知道怎么实现的)。相比DFM是数值的,可以求解没有导函数,以及函数只有数据点的情况,更加普适。在运算量上,说不定也有优势。
误差分析
Error
- round-off error
- truncation error
truncation error
$h>0,x<\xi<x+h;h<0,x+h<\xi<x$
$x\rightarrow y$ 唯一,而 $x\rightarrow y^\ast$ 和 $h$ 的取值相关。FDM求解的是 $y^\ast$ ,选择的映射方式不同,解的值 $y^\ast$ 也不同。
对比求导表达式,当 $h\rightarrow 0$ 时,收敛到理想值。步长 $h$ 绝对值越小,精度越大,运算量越大。
不同的映射方式分为forward difference, backward difference和central difference。他们的误差都是 $f’’(\xi)h$ 。
应用
求解1-D热传导方程
根据表达$\frac{\delta U}{\delta t}$,$\frac{\delta ^2 U}{\delta t^2}$的差分方式,可分为三种方法。
|
时间一阶偏微 |
空间二阶偏微 |
时间基准 |
| Explicit Method |
forward |
center |
$t_n$ |
| Implicit Method |
backward |
center |
$t_{n+1}$ |
| Crank-Nicolson Method |
center |
center |
$t_{n+1/2}$ |
MATLAB仿真
本题的理论解
Explicit Method
Explicit Method最容易实现,计算量最小。
循环实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| Alpha = 1/pi^2;
k = 0.1;
h = 0.1;
r = Alpha*k/h^2;
t = 0:k:2;
x = 0:h:1;
nt = length(t);
nx = length(x);
u = zeros(nx,nt);
u(:,1) = Alpha * sin(pi*x);
for n = 1:nt-1
for j = 1+1:nx-1
u(j,n+1)=(1-2*r)*u(j,n)+r*u(j-1,n)+r*u(j+1,n);
end
end
clf;
mesh(t,x,u);
xlabel('t','FontSize',20);
ylabel('x','FontSize',20);
title({'Explicit Method by Loop'; ...
[' k = ',num2str(k)];...
[' h = ',num2str(h)];...
[' r = ',num2str(r)]})
|
矩阵实现
$U_{n+1}$和$U_n$的维度并不相同。删减$L$的最左最右列变成方阵(还是三对角矩阵)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| Alpha = 1/pi^2;
k = 0.1;
h = 0.1;
r = Alpha*k/h^2;
t = 0:k:2;
x = 0:h:1;
nt = length(t);
nx = length(x);
u = zeros(nx,nt);
u(:,1) = Alpha * sin(pi*x);
d = ones(nx-2,1)*(1-2*r);
e = ones(nx-3,1)*r;
L = full(gallery('tridiag',e,d,e));
for n = 1:nt-1
u(2:nx-1,n+1)=L*u(2:nx-1,n);
end
clf;
mesh(t,x,u);
xlabel('t','FontSize',20);
ylabel('x','FontSize',20);
title('Explicit Method by Matrix')
|
Implicit Method
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| Alpha = 1/pi^2;
k = 0.1;
h = 0.1;
r = Alpha*k/h^2;
t = 0:k:2;
x = 0:h:1;
nt = length(t);
nx = length(x);
u = zeros(nx,nt);
u(:,1) = Alpha * sin(pi*x);
d = ones(nx-2,1)*(1+2*r);
e = ones(nx-3,1)*(-r);
L = full(gallery('tridiag',e,d,e));
for n = 1:nt-1
u(2:nx-1,n+1)=L\u(2:nx-1,n);
end
clf;
mesh(t,x,u);
xlabel('t','FontSize',20);
ylabel('x','FontSize',20);
title({'Implicit Method by Matrix'; ...
[' k = ',num2str(k)];...
[' h = ',num2str(h)];...
[' r = ',num2str(r)]})
|
Crank-Nicolson Method
TODO
运行结果
Explicit Method仅当 $r\leq\frac12$ 时是稳定的,Implicit Method和Crank-Nicolson Method是稳定的。
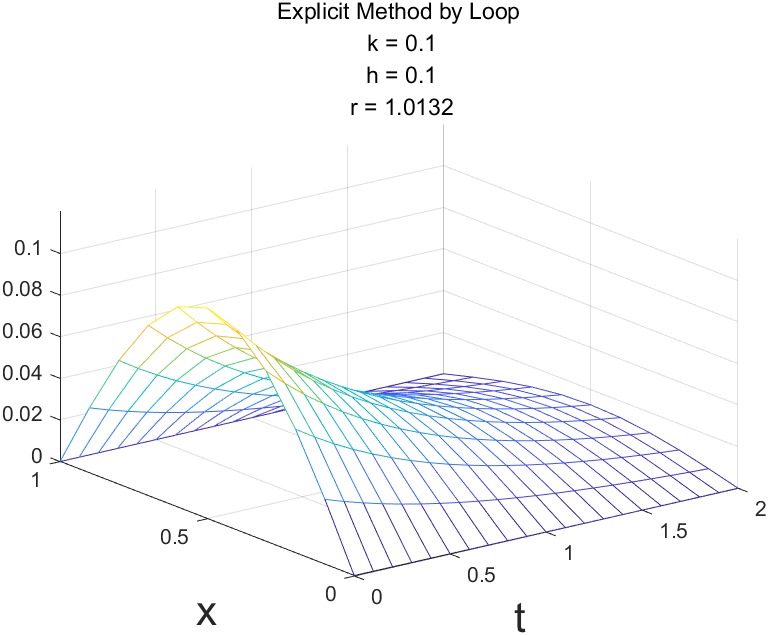
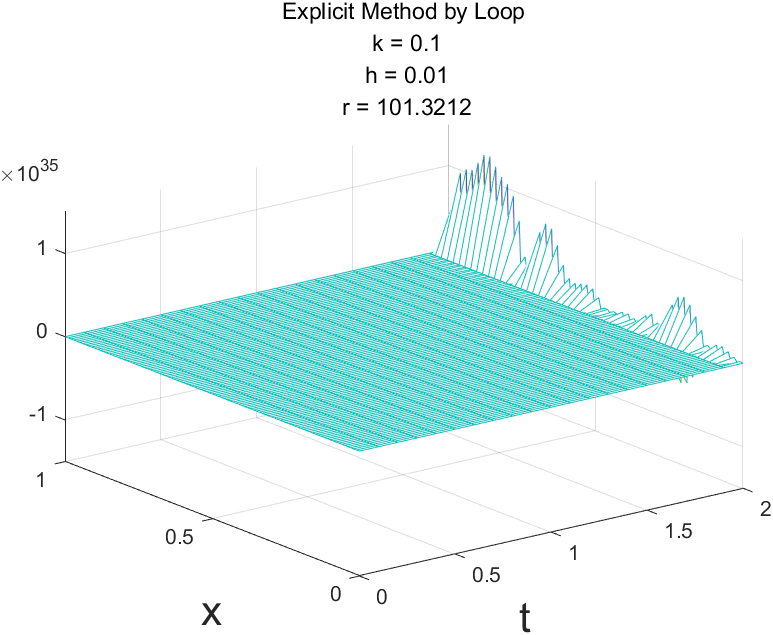
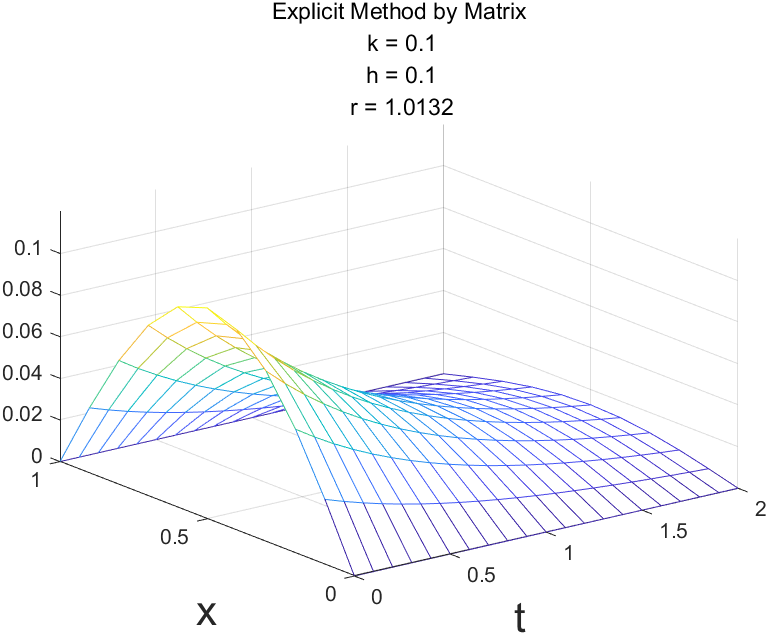
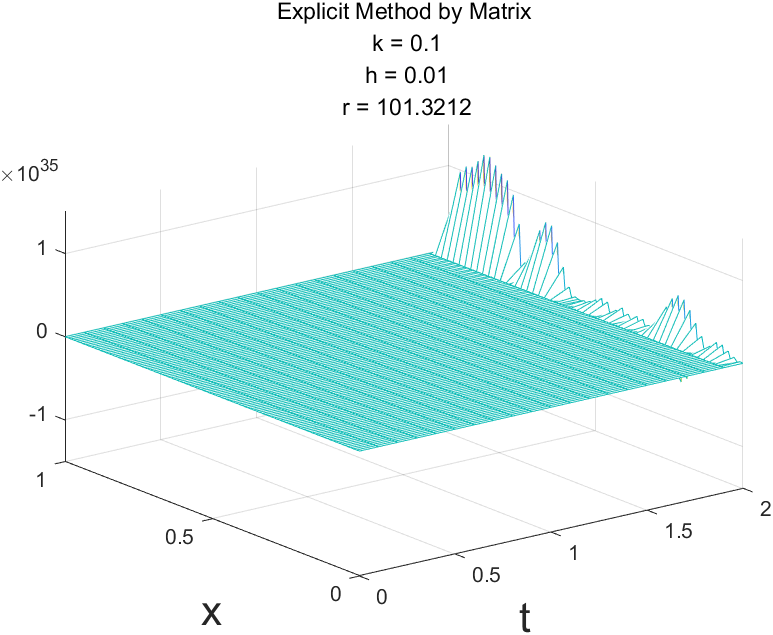
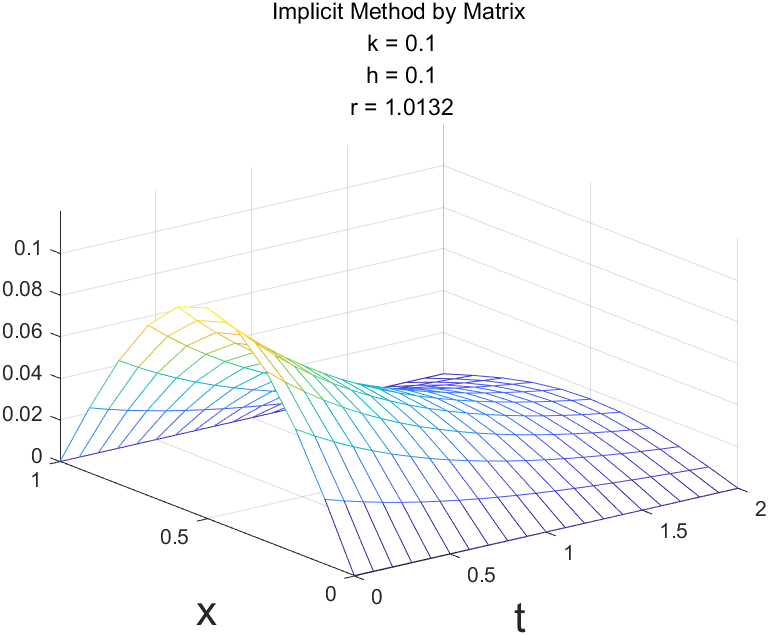
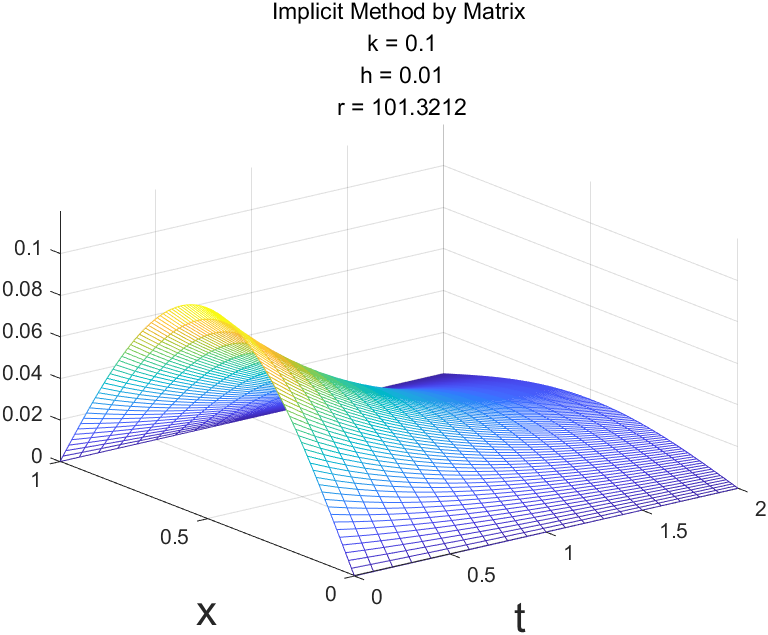
r = 1.0132 Explicit Method没看到不稳定数据?不妨将计算时间范围扩大一些
在编写程序时,状态随着$t$传播的感受十分直观。这与数学上解方程的感觉是不同的,也更加符合公式所描绘的物理图景。
参考
Finite difference method - Wikipedia
Finite difference - Wikipedia






