反直觉的反馈系统

不自恰的反馈

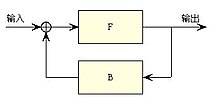
课堂上常常这样介绍反馈：“输出反馈到输入……从而调整了输出”

从电路分析，到信号与系统，再到控制理论。每次听到这样的分析，心中总隐隐感觉不舒服———说明这种解释在某些地方不能很好地自恰。

从物理角度上看，不妨假设这是一个电路系统而反馈元件是一个简单的电阻。信号从输入端口输入的一瞬间，它并不能看到整个系统的全貌，知道哪条路是前向通路，哪条路是反馈回路（这揭示了某种超距作用）。所有的信号通路对它是一视同仁的，它沿着信号通路向前传播，它从前穿过电阻而是从后，这与反馈的思想相背。

从逻辑上分析，Wiki中有这么一段话：

Simple causal reasoning about a feedback system is difficult because the first system influences the second and second system influences the first, leading to a circular argument. This makes reasoning based upon cause and effect tricky, and it is necessary to analyze the system as a whole. As provided by Webster, feedback in business is the transmission of evaluative or corrective information about an action, event, or process to the original or controlling source.

输入影响到输出，输出影响到输入，如此构成了无限循环的逻辑。使用“输出->输入”的反馈逻辑是不符合因果性的。

人为赋予系统意义

即使这种分析思路是不自恰的，但反馈方便理解系统作用，故仍常常以这种方式引入反馈系统。我们人为地为系统赋予了“反馈”的含义。

就像一种系统函数，可以有多种实现结构，不同的结构又有不同的理解。在信号系统相关学科中，很多时候都带有“人为”的痕迹。从系统框图和信号流图中可见一斑。

（注：以下讨论的都是SISO线性系统）

物理上，信号的传播方向和系统物理实现的空间分布相关。系统框图反应系统的理论功能，理论上并不能确定物理上信号的“流向”。大部分的“流向”都是人为赋予信号的意义。

（某些信号的流向还是有意义的，比如系统整体上输入引起输出的因果性。但就如同上文对于反馈的分析，更多系统内部模块或者说子系统的“输入”“输出”都是人为定义的）

我们知道，系统的作用由系统函数（Y-X满足的方程）唯一确定，而系统框图则是将这个方程添加了许多中间变量，拆分成了方程组。如果有m个中间变量，则是由m+1个方程构成的方程组描述这个框图（算上输入输出，一共m+2个变量，联立X的值和方程组可以解出方程组，所以需要m+1个方程）。

但是即使规定了系统的中间变量（也就是描述系统的方程组），系统框图也不是唯一的。这来自于人为规定信号的“流向”。

分析信号流向的关键是相加点和分叉点。前者将多种信号耦合成一种信号，而后者将一种信号分成不同信号。

比如对于方程：

$$x_1+x_2=x_3+x_4$$

相加点是多->一的关系。同一个方程，可以得到不同的相加点结构，比如：

$$\begin{align} \nonumber x_1 & = -x_2+x_3+x_4\\ \nonumber x_2 & = -x_1+x_3+x_4\\ \nonumber x_3 &= x_1 + x_2 -x_4\\ \nonumber x_4 &= x_1 + x_2 -x_3 \end{align}$$

在对同一个方程的不同解释中，就规定了信号的“流向”。

对于信号流图也一样，信号流图则是将框图中相加点和分叉点合并了节点。节点将多种输入信号耦合，并且可以有多个输出，所有的输出都是相同信号。

参考

Feedback Wiki