信号经过门限判决，损失了非常多的特征，是不可能彻底恢复出原始信号的。不过我好奇经过门限判决后，究竟有多少特征被破坏，而多少特征得以保留了下来？也可以说，我们究竟可以把信号恢复到什么程度？

门限判决，以5000作为阈值

门限判决是多对一的映射操作。为了增加信号可以恢复的程度，我们缩小原始信号范围，只讨论音频信号的恢复。

恢复信号的数学条件

从门限判决的过程中，能直观得提取出一些恢复信号需要满足的特征：

其次一些针对音频信号的自然条件：

算法评价

我们以一个算法能多大程度恢复门限判决带来的损失（恢复率）作为评价标准

以频谱差的二范数定义门限判决带来的损失 $e_{threshold} = ||f_t-f_0||_2$

$f_0$是原始信号频谱的模，而$f_t$是门限判决之后的频谱的模。

相似地，得到恢复信号相对原始信号的损失 $e_{recover} = ||f_r-f_0||_2$

则恢复率定义为 $recover\_rate = \frac{e_{threshold}-e_{recover}}{e_{threshold}}\times 100\%$

思路

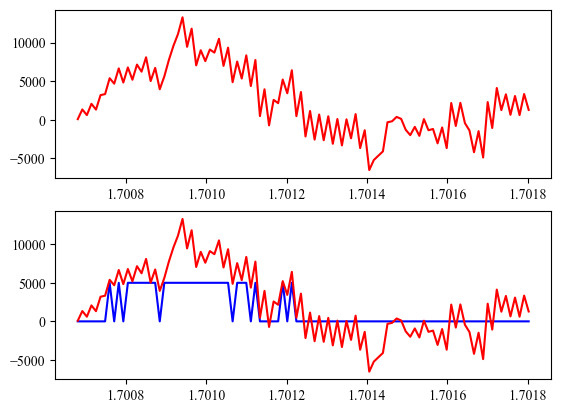
在一个相对短的时间内，假设信号频率是不变的，我们用余弦信号近似表示信号。可以通过门限判决序列每段[1,1,1…1,0,0,0…0]子序列的长度和占空比确定余弦的幅度和频率。

恢复效果，红色原始信号，蓝色恢复信号

问题

在短时间内，信号是由多个频率组成的，这个假设并不成立，因此只能复原出信号的主要变化趋势，无法复原出次波。

并且当占空比大于50%时，会出现倒相问题，幅度计算为负值，不满足（1）和（5）的条件。

恢复率

以《手心的蔷薇》60~65s的音频作测试，恢复率在 -2.19%，这是恢复后的效果，也别有韵味。

相比门限判决信号，误差反而更大了。不过判决后的信号因为只有两个值，播放出来是纯粹的噪声。

思路

如果对门限判决的二制序列做差分，则得到了由0,1,-1构成的序列。阈值 $y=threshold$ 在图像中是一根平行于时间轴的横线，而1,-1则代表信号穿过阈值的方向，1是从下方往上方穿越，而-1是从上方往下方穿越。

我们并不直接恢复原始信号，而是恢复原始信号的导数，再加以相应的约束条件确定初值（比如（2）），即可得到恢复信号。

导数的构建为了满足约束（1），需要保证导数值在1,-1之间的区间内积分（数值和）为0，这是一个函数拟合问题，最简单的思路便是每段之间用一次函数代替，那么原始信号便是分段的二次函数的集合。

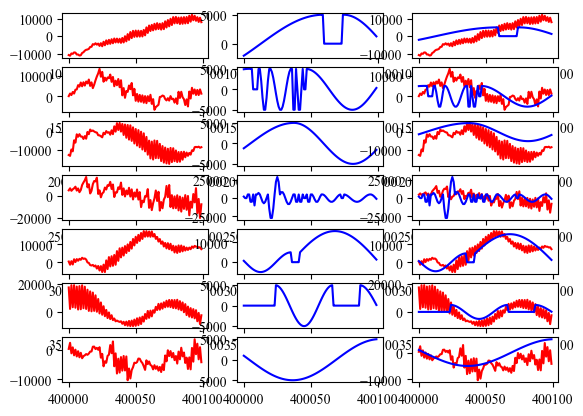
问题

恢复结果

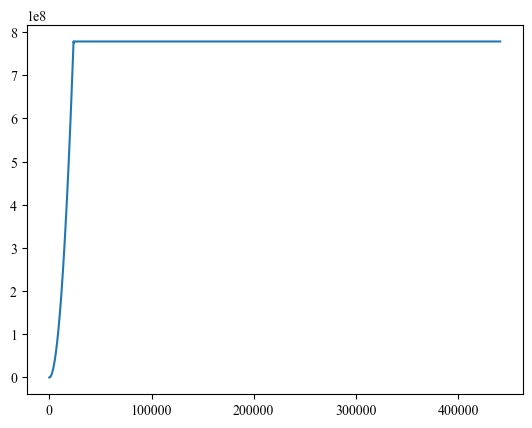
并不满足幅度条件（3），恢复信号是在阈值上下振荡，近似直流信号。

思路

既然余弦恢复法只能恢复出主要频率，便让门限信号经过一个低通滤波器分出变化缓慢的主要序列和变化较快的次波序列，再分别用余弦法恢复，最后叠加得到恢复信号。

思路

使用1次函数拟合函数很大一部分原因是个人数学能力不够，二次函数构建法没有考虑赋值的约束条件。能否使用人工智能去拟合满足约束的函数？

思路

亚采样的过程也是一个多对一的映射，而压缩感知是求采样方程的稀疏解。能否可以借鉴压缩感知的思路？

门限判决后将每时刻的数据压缩到了1bit,可以作为一种有损压缩或者调制的方法。就像本文中歌曲的例子，每个时刻原始信号是2Byte,压缩率能达到16x(当然本身mp3格式也是经过压缩的，不能这么简单粗暴的计算)。

本篇博客讨论的是单阈值的恢复方法，如果推广到多个阈值，即可作为量化误差的恢复方法（量化是在幅度域上均匀地“采样”，根据压缩感知的思想，不均匀的采样也能搞搞）。